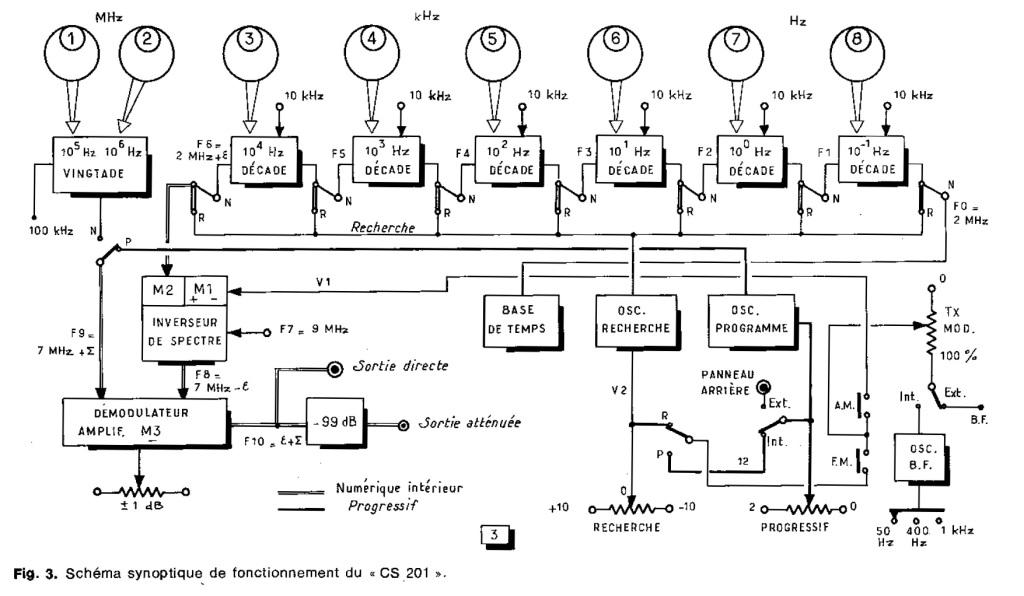
De quoi s'agit-il ?

La figure ci-dessus représente le principe de fonctionnement du synthétiseur Adret 201. Mais pourquoi présenter un synthétiseur vieux de plus de 40 ans?

C'est l'idée du fonctionnement de ce synthétiseur qui est très intéressante.

Essayons d'abord de comprendre comment fonctionne la synthèse de fréquences...

«décade» , «vingtade» , «millade» , «centmillade» .... Roger Charbonnier aimait introduire un certain vocabulaire qui lui était propre. Qu'en est-il ?

Le circuit de synthèse de l'Adret 201 contient 6 décades identiques et une vingtade. Une décade élabore une puissance de 10 de la fréquence chiffre par chiffre de 0 à 9.

Une vingtade élabore 2 puissances de 10 successives chiffre par chiffre de 0 à 99.

De même, lorsque nous verrons le petit frère du 201, l'Adret 201SB, nous aurons affaire à une millade, unité qui élabore 3 puissances de 10 successives.

L'adret 303 comporte également une millade, unité permettant de synthétiser entre autre le millième de Hz directement par commande en face avant.

L'adret 2400 comporte une unité d'insertion décimale appelée «centmillade» qui élabore les chiffres de fréquences de rang 10E0 Hz à 10E4 Hz.

Au regard des définitions précédents, on se serait attendu plutôt au terme «centade» au lieu de «vingtade»...

Ce synthétiseur couvre les fréquences de 0.1 Hz à 2 MHz. La synthése des fréquences est appelée itérative, puisque chaque chiffre de la fréquence programmée est élaboré séparément et à l'identique via ce que l'on appelle des décades (mot de Roger Charbonnier), qui sont des unités d'insertion décimales (UID dans la littérature). Elles sont au nombre de 6 pour les chiffres de 0.1 Hz à 10E4 Hz. Les 2 chiffres des 100 000Hz et 10E6 Hz sont insérés par une vingtade.

Reprenons l'article pas à pas...

Comme la figure le montre, il s'agit de synthétiser la fréquence 1 234 567,8 Hz= a bcd efg,h Hz.

Ici, a=1 - b=2 - c=3 - d=4 - e=5 - f=6 - g=7 - h=8

Définitions: La fréquence F0=2MHz est issue de la base de temps. F1 est la fréquence générée par le 1ère décade et injectée à la seconde. F2 est la fréquene générée par la seconde décade et injectée à la 3ième, etc..

Le rôle des décades est de générer, pour les décades supérieures, des fréquences modifiés de la façon suivante: la première décade reçoit la fréquence porteuse F0=2Mhz, extrêmement précise fournie par le pilote, à laquelle s'ajoute autant de multiples de 10kHz que le chiffre programmé. La première décade génère donc

F1=2 080 000Hz.

Mais ceci s'effectue de la façon suivante dans une décade. La sous-porteuse produite par la base de temps F0= 2MHz est d'abord divisée par 10. Dans la décade se trouve une boucle à vérouillage de phase qui génère une fréquence de 1.8 MHz majorée de h fois la fréquence de référence de 10Khz. L'oscillateur de cette boucle génère donc une fréquence de 1.8 MHz + h x 10 kHz. Un mélangeur M effectue la somme de cette fréquence avec la fréquence de 200 kHz précédente. On a donc une fréquence,

pour la première décade,

F1= 2 000 000 + 10 000xh Hz

qui est injectée à la décade suivante, décade des Hz. divise par 10 F1 et ajoute 1.8 MHz avec autant de multiples de 10kHz que le chiffre programmé pour cette décade, soit donc:

pour la deuxième décade,

F2 = F1/10 + 1.8 MHz + 10 000xg = 208 000 + 1 800 000 + 10 000x7 = 2 078 000 Hz,

Et, pour la troisième décade,

F3= F2/10 + 1.8 MHz + 10 kHz xf = 207 800 + 1 800 000 + 60 000 = 2 067 800 Hz

pour la quatrième décade,

F4= F3/10 + 1.8 MHz + 10 kHz x e = 206 780 + 1 800 000 + 50 000 = 2 056 780 Hz

pour la cinquième décade,

F5= F4/10 + 1.8 Mhz + 10 kHz x d = 205 678 + 1 800 000 + 40 000 = 2 045 678 Hz

pour la sixième (et dernière) décade, puiqu'on atteint le dixième de Hz attendu

F6= F5/10 + 1.8 Mhz + 10 kHz x c = 204 567,8 + 1 800 000 + 30 000 = 2 034 567,7 Hz

Au total, F6 est la somme du 2Mhz initial avec tous les incréments successifs, ce qui peut s'écrire F6 = 2 MHz + (somme_incréments)

Quelle est la plage de fréquences possible de F6 ?

Les incréments maximaux étant les chiffres 9, la fréquence minimale est 2 MHz (tous les incréments nuls) et la fréquence maximale est 2 099 999,9 Hz. Les pas étant de 0.1Hz, on a un million de fréquences possibles.

A ce stade, nous n'avons pas encore synthètisé la fréquence finale...

On réalise ensuite un battement soustractif de F6 avec du 9 MHz, issu de la base de temps.

Ce qui donne une fréquence F7 = 9 MHz - (2MHz + (somme_incréments) = 7 MHz - (somme_incréments)

F7 = 7 000 000 - 34 567,8 = 6 965 432,2 Hz

La vingtade élabore la centaine de kilohertz et le million de Hz. Elle fournit une porteuse de 7Mhz majorée d'un nombre de pas de 100 kHz qui correspondent aux chiffres des centaines de milliers de Hz et des millions de Hz, soit de 0 à 19 fois 100 kHz.

Avec la fréquence programmée au départ, cela donne:

F8= 7 MHz + 100 kHz x 12 = 8 200 000 Hz = 7 MHz + (gros_incréments)

On effectue ensuite la battement soustractif de cette fréquence avec F7:

F9= F8 - F7 = 7MHz + (gros incréments) - 7 Mhz - (somme_incréments) = (gros incréments) - (somme-incréments)

F9 = 8 200 000 - 6 965 432,2 = 1 234 567,8 Hz

fréquence tant attendue!

Maintenant, pourquoi est-ce que ça marche? comment se fait-il que cet artifice d'incrémentation, de mélange additif et soustratif finisse par donner une fréquence correcte?

Roger Charbonnier nous donne là une belle leçon d'arithmétique.

Les autres Adret qui suivirent fonctionnent sur le même principe initial, mais c'est de plus en plus complexe. Il y en a un même, pour lequel, il ne donne pas l'astuce arithmétique qui permet dans l'étage final d'obtenir la fréquence programmée. Et là, c'est un tour de force que de comprendre ce qui se passe. Pour autant, j'ai cherché longtemps sans trouver...et puis un jour, j'ai fini par trouver sans chercher...

On l'aura compris, l'aventure Adret n'est pas seulement une aventure matérielle pour laquelle il s'agit de sauvegarder un certain patrimoine matériel français, c'est avant tout une aventure intellectuelle, où le génie français, ou à tout le moins, le génie qui existait autrefois, mérite qu'on y consacre un peu de temps pour s'en rappeler.

Les calculs précédents constituent une trame d'un bon fonctionnement cérébral pour ceux qui se donnent la peine de les comprendre. Mais où sont-ils ?

(suite....)